Toán lớp 12 – Công thức tính thể tích khối chóp đầy đủ, chi tiết nhất

Thể tích khối chóp là một trong những công thức mà các em học sinh khối 12 cần nhớ rõ vì chúng thường xuất hiện trong toán học. Để có thể vận dụng tốt vào bài tập, Học Thông Minh đã tổng hợp thêm các bài tập minh họa đơn giản, giúp các em có thể hiểu và nhớ nhanh hơn. Hãy cùng khám phá ngay nhé.

1. Thể tích khối chóp là gì?

 

Để hiểu hơn về thể tích khối chóp, chúng ta cần tìm hiểu khái niệm về hình chóp.

1.1 Khối chóp là gì

 

Khối chóp còn có tên gọi khác là hình chóp. Hình có mặt bên là các tam giác cùng chung một đỉnh và mặt đáy là một đa giác bất kỳ. Những tam giác kết hợp chung một đỉnh được gọi là đỉnh của khối chóp.

1.2 Đặc trưng của khối chóp

 

Đường thẳng vuông góc với mặt đáy và đi ngang qua đỉnh của hình chóp được gọi là đường cao của đỉnh. Dựa vào đáy đa giác là gì, từ đó ta suy ra tên của hình chóp.

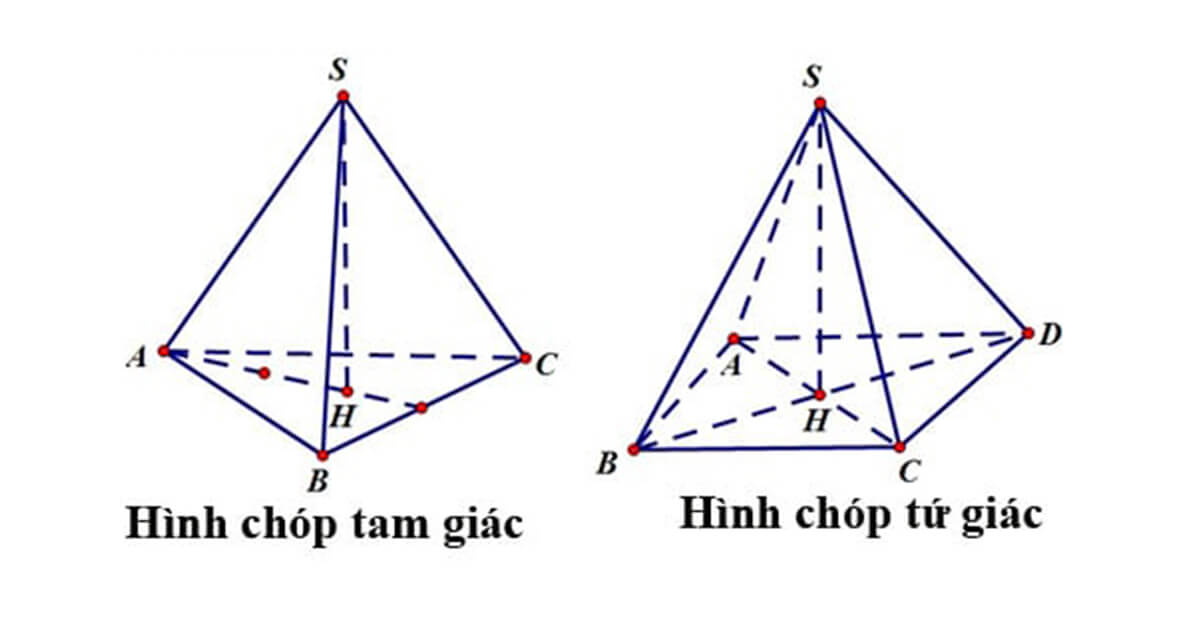
Ví dụ: Hình chóp có đáy là tam giác thì đó là hình chóp tam giác, hình chóp có đáy là tứ giác thì đó là hình chóp tứ giác.

Ngoài khối chóp tam giác thì còn có những khối chóp đặc biệt mà các bạn học sinh cần nắm rõ đó là khối chóp tứ diện đều và khối chóp tứ giác đều.

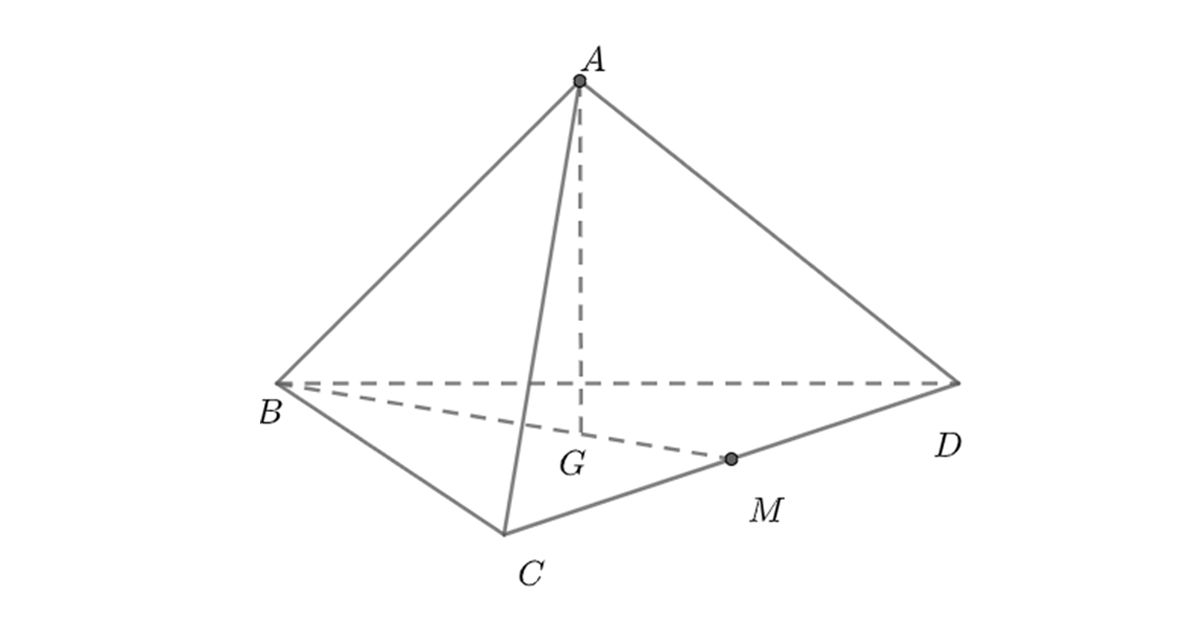
Khối chóp tứ diện đều

Dấu hiệu nhận biết khối chóp tứ diện đều là các mặt bên đều là những tam giác đều, các cạnh cũng bằng nhau. Với OA là đường cao của hình chóp đó, OA vuông góc với mặt phẳng CBD.

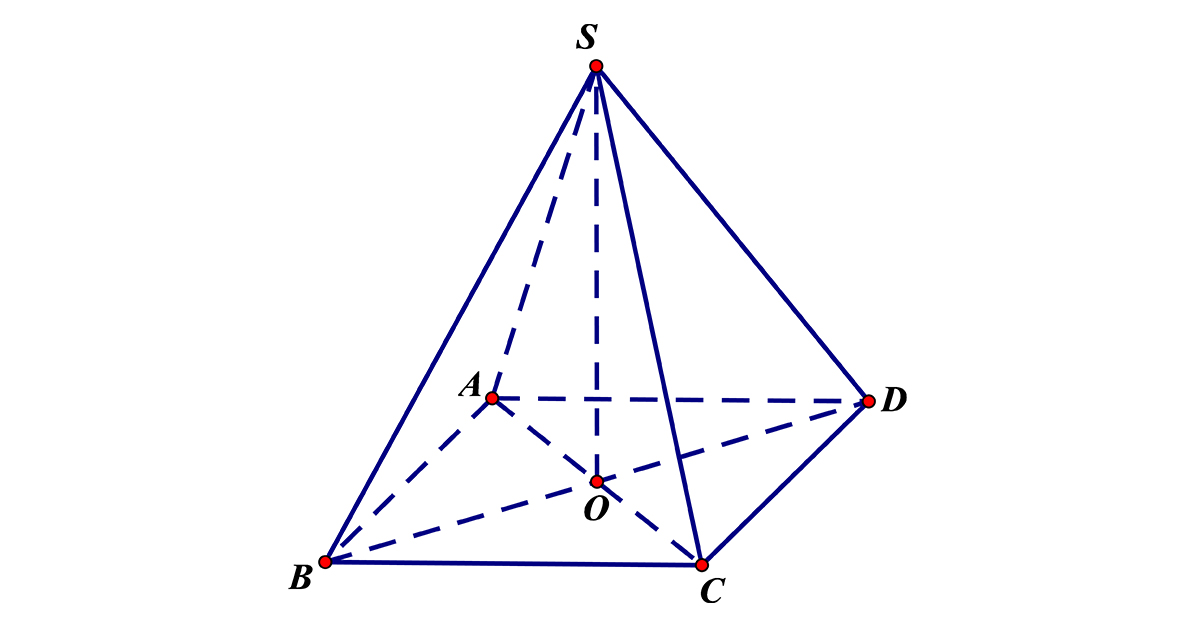
Khối chóp tứ giác đều

Đây là khối chóp có những cạnh bên bằng nhau, mặt đáy là đa giác dạng hình vuông có tâm 0, đường cao OS vuông góc với mặt đáy (ABCD)

 

2. Tính chất cơ bản của khối chóp

Hình có các cạnh bên bằng nhau hợp với mặt đáy một góc bằng nhau thì đường cao chính là tâm đường tròn ngoại tiếp của mặt đáy hình chóp này.

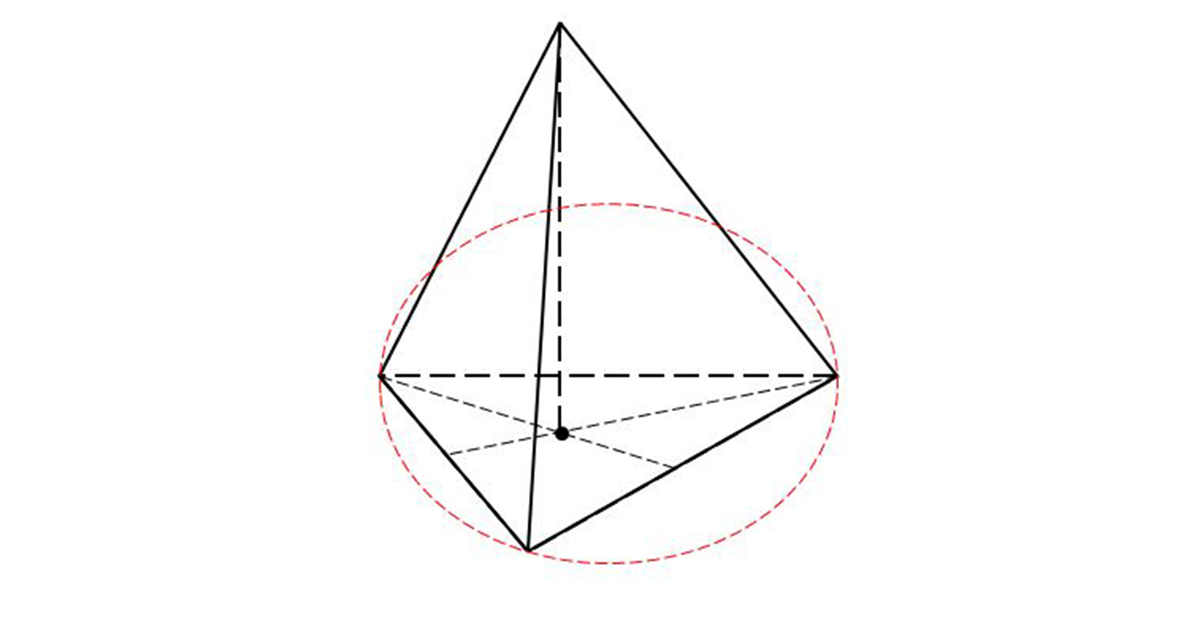
Các cạnh bên có các đường cao của các mặt bên xuất phát từ một đỉnh đều bằng nhau hay các mặt bên hợp với đáy một góc bằng nhau thì chân đường cao là tâm đường tròn nội tiếp với mặt đáy.

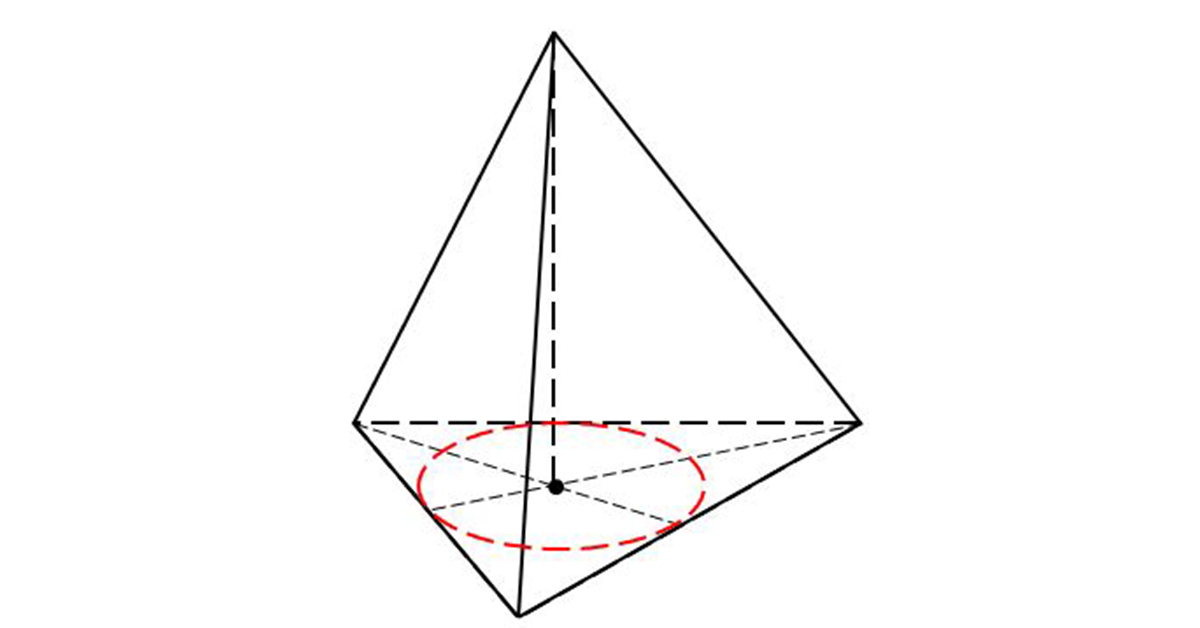
Các mặt chéo hoặc các mặt bên vuông góc với mặt đáy thì đường cao hình chóp là đường cao của các mặt chéo hoặc một mặt bên đó.

 

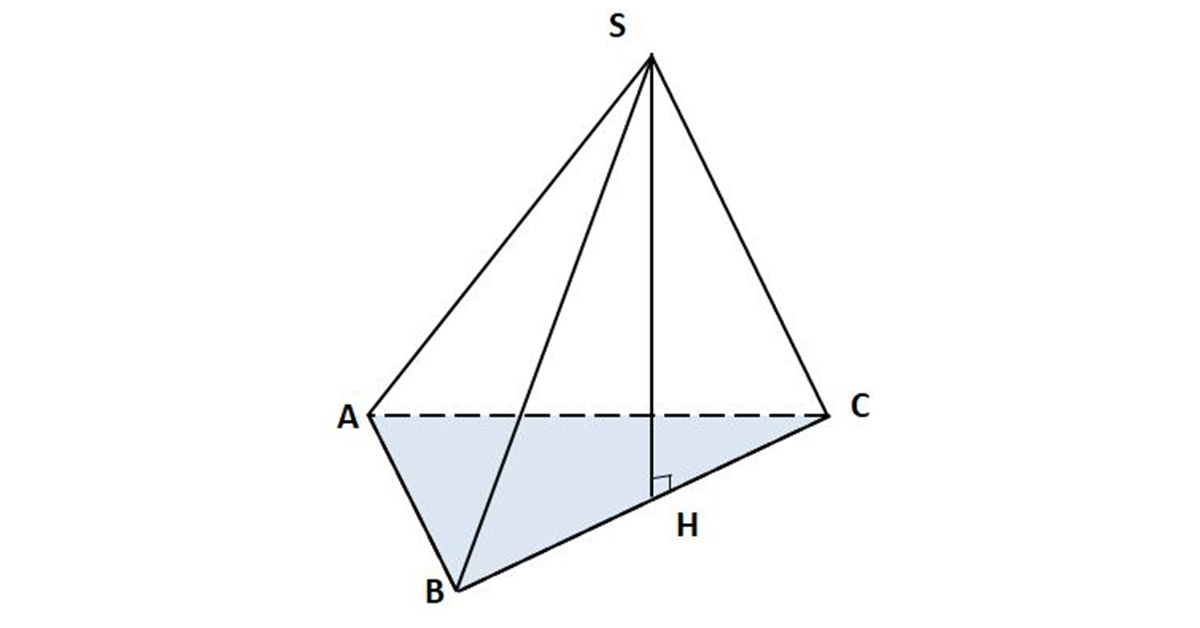
3. Công thức tính thể tích hình chóp

Thể tích của khối chóp được phát biểu như sau: Thể tích hình chóp bằng một phần ba mặt đáy nhân với chiều cao của hình chóp.

Công thức:

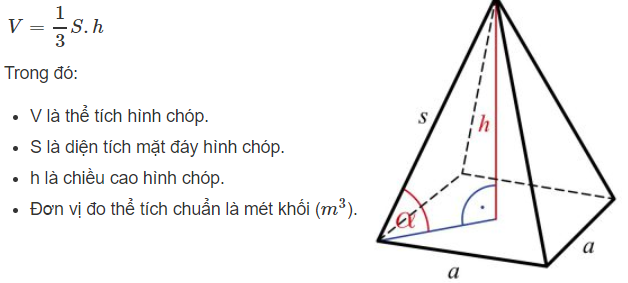
4. Công thức thể tích khối chóp tam giác đều và tứ giác đều

 

4.1 Khối chóp tam giác đều

 

Là hình chóp có tất cả các cạnh bên bằng nhau, đáy là tam giác. Chân đường cao là trọng tâm của tam giác đáy.

Ví dụ: Cho hình chóp đều S.ABC cạnh đáy bằng a và cạnh bên có độ dài bằng 2a. Bạn hãy chứng minh rằng chân đường cao kẻ từ S của hình chóp là tâm của tam giác đều ABC. Hãy tính thể tích của khối chóp tam giác đều S.ABC.

Bài giải:

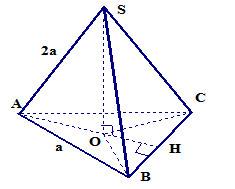
Dựng SO⊥ ΔABC, Ta có SA = SB = SC suy ra OA = OB = OC

Vậy O là tâm của tam giác đều ABC.

Ta có:

AO = ⅔.AH = ⅔. a√3/2 = a√3/3

Tam giác ABC đều nên tam giác SAO vuông tại O, áp dụng định lý Pi-ta-go ta có: SO² – OA² = 11a²/3

=>SO = a√11/√3

=>V = ⅓.S(ABC).SO = a³√11/12

>>Đọc thêm: Tất tần tật nội dung về khối đa diện

4.2 Khối chóp tứ giác đều

 

Là hình chóp có tất cả các cạnh bên bằng nhau, có đáy là hình vuông, chân đường cao là tâm của hình vuông.

Ví dụ: Cho khối chóp đều S.ABCD có đáy vuông cạnh a. Các cạnh bên dài 2a. Tìm thể tích hình chóp S.ABCD 

Bài giải:

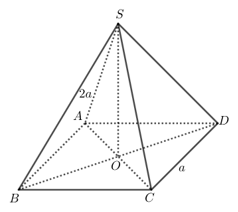
Gọi O là tâm của hình vuông ABCD. Ta có SO ⊥ (ABCD)

BD = a√2 =>OD = a√2/2 =>OD = a√2/2

Áp dụng định lý Pi-ta-go cho tam giác SOD ta được:

SO = a√14/2

Diện tích ABCD là a²

=> Thể tích  S.ABCD = ⅓.a√14/2.a² = a³√14/6

>>Đọc thêm: Cách học giỏi môn toán 12

5. Bài tập củng cố kiến thức thể tích khối chóp

 

Câu 1: Cho hình chóp S.ABC có đáy abc là tam giác vuông cân C ở B, AC=a√2, SA vuông góc với mặt phẳng (ABC), SA = a. Thể tích S.ABC là gì?

A. a³/6

B. a³/3

C. 7a³/6

D. 5a³/6

 

Câu 2: Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = 2a, AD = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa SC và mặt phẳng S.ABCD bằng 60º. Tính thể tích khối chóp S.ABCD

A. a³/15

B. 2a³√15/3

C. 7a³/6

D. a³

 

Câu 3: Cho khối chóp S.ABC có ABCD là hình vuông cạnh a; SA ⊥ (ABCD). Góc giữa mặt phẳng (SBD) và (ABCD) bằng 30º . Tính thể tích S.ABCD

A. a³√3/3

B. a³√2/3

C. a³√6/18

D. a³√6/9

 

Câu 4: Cho khối chóp S.ABCD có ABCD là hình chữ nhật; AC=2AB=2a ; SA vuông góc với mặt phẳng đáy. Tính thể tích S.ABCD biết rằng SD=a√5.

A. a³√5/3

B. a³√15/3

C. a³√6

D. a³√6/3

 

Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích hình chóp S.ABC biết rằng SC=a√3

A. 2a³√6/9

B. a³√6/12

C. 2a³√6/4

D. a³√3/4

 

Ngoài ra các em có thể luyện tập thêm các dạng toán tính thể tích khối chóp tại đây.

Vừa rồi là toàn bộ những nội dung về định nghĩa khối chóp, tính chất và công thức tính thể tích khối chóp mà Học Thông Minh chia sẻ đến các bạn học sinh cuối cấp. Mong rằng các bạn sẽ ghi nhớ và áp dụng tốt vào bài tính toán của mình nhé. Để nắm chắc kiến thức liên quan đến học phần này, bạn có thể tham khảo thêm các dạng bài luyện thi trắc nghiệm online nhé.