Trong môn Toán, phần Hình học ở bậc THCS, kiến thức về hình bình hành, đặc biệt là cách tính diện tích hình bình hành, chu vi hình bình hành là nội dung mà các bạn học sinh cần ghi nhớ để áp dụng vào giải các bài tập thường ngày hay trong các kỳ thi.

Mặc dù đã được làm quen với hình bình hành từ trước đó, song không phải học sinh nào cũng có thể hiểu và nắm vững các kiến thức liên quan và vận dụng thành thạo vào tính toán. Do đó, Học Thông Minh đã tổng hợp một số kiến thức hình bình hành cơ bản trong bài viết dưới đây, với mong muốn hỗ trợ tốt nhất cho các em trong quá trình học tập. Mời các em cùng tham khảo nhé!

1. Khái niệm hình bình hành:

Hình bình hành là khái niệm dùng để chỉ một hình tứ giác được tạo thành khi có hai cặp đường thẳng song song cắt nhau. Hình bình hành còn được biết đến là một dạng đặc biệt của hình thang.

Trong không gian 3 chiều, hình khối lục diện  chính là khối tương đương với hình bình hành. 

Đơn giản hơn, có thể hiểu hình bình hành là một tứ giác trong đó các cạnh đối song song với nhau. 

Ví dụ : Nếu hình bình hành đã cho được gọi là MNPQ, từ đó ta có: 

  • Cạnh MN đối diện và song song với cạnh PQ 
  • Cạnh MQ đối diện và song song với cạnh NP

1.1. Hình bình hành có những tính chất nào?

Hình bình hành mang các tính chất sau:

  • Các cạnh đối diện của hình bình hành song song với nhau và bằng nhau.
  • Các góc đối diện của hình bình hành bằng nhau.
  • Hình bình hành có 2 đường chéo được xác định cắt nhau tại trung điểm của mỗi đường.

1.2. Dấu hiệu nhận biết hình bình hành:

Hình bình hành được biết đến là một tứ giác đặc biệt. Để nhận biết hình bình hành, chúng ta căn cứ vào các dấu hiệu như sau:

  • Nếu một tứ giác có hai cặp cạnh đối diện song song nhau thì tứ giác đó là hình bình hành.
  • Nếu một tứ giác có các cạnh đối diện bằng nhau thì tứ giác đó là hình bình hành.
  • Nếu một tứ giác có hai cạnh đối diện vừa song song và vừa bằng nhau thì tứ giác đó là hình bình hành.
  • Nếu một tứ giác có các góc đối diện bằng nhau thì tứ giác đó là hình bình hành.
  • Nếu tứ giác có hai đường chéo được xác định cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình bình hành.

Chú ý: Hình thang được gọi là hình bình hành trong trường hợp:

  • Hình thang đó có hai cạnh bên song song với nhau 
  • Hình thang đó có hai cạnh đáy bằng nhau 

1.3. Diện tích hình bình hành là gì? 

Diện tích hình bình hành được hiểu là toàn phần mặt phẳng mà ta có thể thấy được của hình bình hành đó.

Diện tích hình bình hành được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy được của hình bình hành.

1.4. Chu vi hình bình hành là gì?

Chu vi của hình bình hành được tính bằng bằng tổng độ dài của 4 cạnh của hình bình hành đó. Hay nói cách khác, chu vi hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ. 

Để học tốt các môn khi vào lớp 10 các em có thể luyện bài tập trắc nghiệm lớp 10 tại Học Thông Minh.

2. Cách tính diện tích hình bình hành

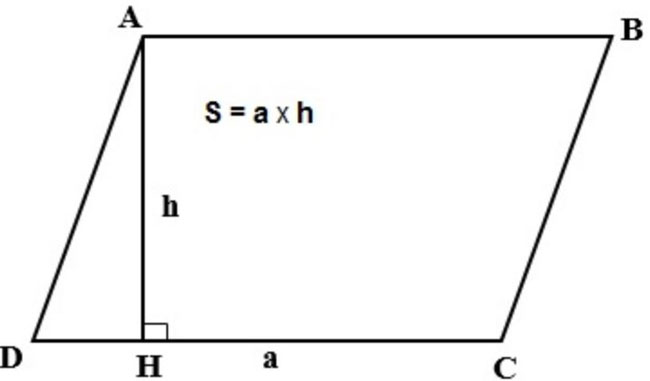
Diện tích hình bình hành được tính theo công thức sau:  

S = a.h

Trong đó:

  • a: là ký hiệu cạnh đáy của hình bình hành
  • h: là ký hiệu chiều cao (được nối từ đỉnh tới đáy của hình bình hành đó)

Diễn đạt theo cách khác dễ nhớ hơn, muốn tính diện tích hình bình hành, ta lấy cạnh đáy nhân với chiều cao của hình bình hành đó.

công thức tính diện tích hình bình hành
công thức tính diện tích hình bình hành

Ví dụ cụ thể: Cho một hình bình hành với chiều dài cạnh đáy CD = 10cm và chiều cao nối từ đỉnh A xuống cạnh CD dài 5cm. Yêu cầu: tính diện tích của hình bình hành ABCD đã cho? 

Hướng dẫn trả lời: 

Ta có: 

  • Chiều dài cạnh đáy CD (a) = 10cm
  • Chiều cao hình bình hành (h) được nối từ đỉnh A xuống cạnh đáy CD = 5cm

Áp dụng công thức tính diện tích hình bình hành, suy ra ta được: 

S (ABCD) = a x h = 10 x 5 = 50 cm2

Đáp án: Diện tích của hình bình hành ABCD đã cho là 50 cm2

Tuy nhiên, trên đây là một ví dụ rất đơn giản để các bạn hiểu và biết cách vận dụng cơ bản công thức tính diện tích hình bình hành vào quá trình giải các bài toán. Trong trường hợp yêu cầu bài toán phức tạp hơn, các bạn cần linh hoạt vận dụng thêm mối tương quan giữa các thành phần trong một công thức cũng như các công thức khác để có thể giải quyết bài toán theo yêu cầu. 

Khi đã nắm chắc kiến thức diện tích và chu vi hình bình hành các em có thể xem phương pháp giải phương trình bậc nhất một ẩn dễ hiểu nhất mà Học Thông Minh chia sẻ nhé

– Tính diện tích hình bình hành như thế nào khi biết hai đường chéo?

Trong trường hợp đề bài toán chỉ cho một số liệu cụ thể về độ dài của hai đường chéo thì chắc chắc sẽ rất khó để chúng ta có thể giải được. Vì thế, thông thường, đề bài sẽ bổ sung thêm thông tin về góc giữa hai đường chéo đi kèm. Ví dụ thể như sau:

Cho một hình bình hành MNPQ có MP và NQ là hai đường chéo, giao điểm của hai đường chéo được ký là O và số đo góc MON được tạo bởi hai đường chéo. Như vậy, cách tính diện tích hình bình hành khi biết độ dài hai đường chéo như sau: 

1/2.MP.NQ.Sin(MON) = 1/2.MP.NQ.Sin(MOQ)

  • Công thức tổng quát tính diện tích hình bình hành khi biết hai đường chéo như sau: 

S = 1/2.c.d.sinα

Trong đó:

  • c, d lần lượt là độ dài của hai đường chéo hình bình hành (hai đường chéo này có cùng đơn vị đo)
  • α là góc được tạo ra bởi hai đường chéo.

Xem thêm: Học giỏi toán thì làm nghề gì

3. Cách tính chu vi hình bình hành 

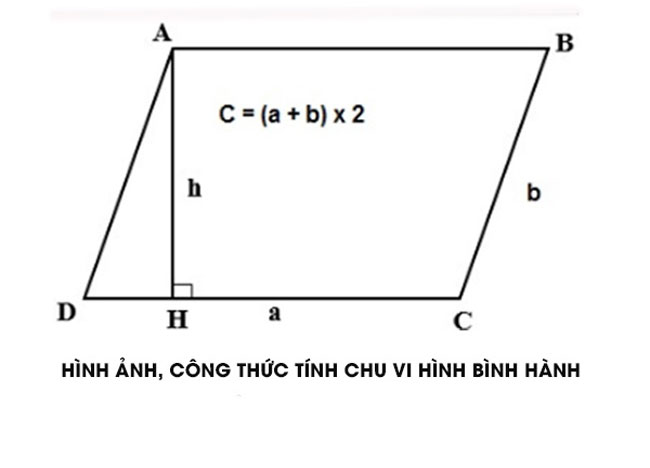
– Chu vi hình bình hành được tính theo công thức sau: 

C = (a+b) x 2

Trong đó:

  • C: là ký hiệu chỉ chu vi hình bình hành
  • a và b: là ký hiệu chỉ hai cạnh bất kỳ của hình bình hành đó

 

Cách tính chu vi hình bình hành
Công thức tính chu vi hình bình hành

Ví dụ cụ thể: Cho hình bình hành ABCD, trong đó, cạnh AB có chiều dài bằng 8cm và cạnh BC có chiều dài bằng 6cm. Hỏi chu vi của hình bình hành ABCD đã cho bằng bao nhiêu?

Hướng dẫn trả lời:

Ta có: 

  • Chiều dài cạnh AB (a) = 8cm 
  • Chiều dài cạnh BC (b) = 6cm

Áp dụng công thức tính chu vi hình bình hành, suy ra ta được:

C = (a +b) x 2 = (8 + 6) x 2 =14 x 2 = 28 cm

Đáp án: Chu vi của hình bình hành ABCD là 28cm. 

Như vậy, bài viết trên đây đã tổng hợp một cách hệ thống và chi tiết các kiến thức liên quan đến hình bình hành, bao gồm khái niệm, tính chất, dấu hiệu nhận biết cũng như cách tính diện tích và cách tính chu vi của hình bình hành. 

Thông qua bài viết này, trắc nghiệm Học Thông Minh mong rằng các bạn học sinh đã có thể nắm được một cách cơ bản và ghi nhớ được phần kiến thức quan trọng này để áp dụng trong việc giải các bài tập, để phần Toán hình học không còn là nỗi “ám ảnh” với các bạn nữa nhé!